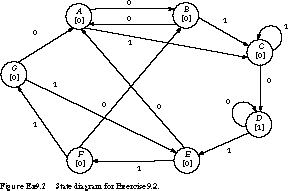
1. (State Reduction) Use the implication
chart method to reduce the 4-bit string recognizer state diagram of Figure
9.2. (State Reduction) Given
the state diagram in Figure Ex9.2, obtain an equivalent reduced state diagram
containing a minimum number of states.

You may use row matching or implication charts. Put your final answer
in the form of a state diagram rather than a state table. Make it clear
which states have been combined.
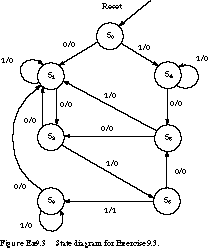
3. (State Reduction) Given
the state diagram in Figure Ex9.3, determine which states should be combined
to determine the reduced state diagram. You may use row matching or implication
charts.
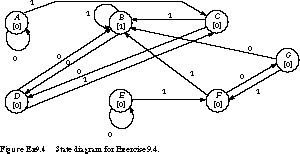
4. (State Reduction) Given
the state diagram in Figure Ex9.4, draw the fully reduced state diagram.
State succinctly what strings cause the recognizer to output a 1.
5. (State Reduction) Starting
with the state diagram of Figure Ex9.5, use the implication chart method
to find the minimum state diagram.
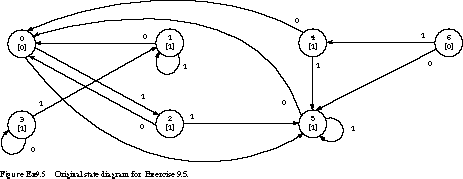
Which of the original states are combined?
6. (State Assignment) Given
the state diagram in Figure Ex9.6, implement a state assignment using the
following techniques:
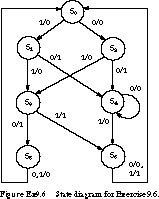
Minimum bit change heuristic
State assignment guidelines Show your assignment in a state map. Explain the rationale for your state assignment.
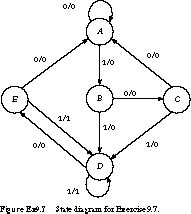
(State Assignment) Given
the state diagram in Figure Ex9.7, select a good state assignment, justifying
your answer in terms of the state assignment guidelines.
8. (State Assignment) One
method for state assignment is to exhaustively enumerate all the possible
state assignments. Given the traffic light controller symbolic state table
of Figure 9.20, use espresso to evaluate all 24 possible 2-bit
encodings of the states. Using literal count as your metric, what is the
optimal encoding?
9. (State Assignment) Using
a logic minimization tool like espresso, try some random encodings
of the traffic light controller that are nondense. That is, map
the four states into eight (3 bits) or sixteen
(4 bits) possible states. How do they compare
in terms of literal count to the encodings found in the previous question?
How many state assignments are possible in these two nondense encodings?
Derive a formula for it if you can.
10. (State Assignment) Given
the next-state function of the finite state machine shown in Figure Ex9.10,
use the implication chart method to find the most reduced state diagram.
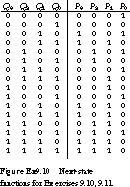
11. (State Partitioning) Show
how to partition the next-state functions of Figure Ex9.10, P3,
P2, P1, P0, into two groups, each of which depends
on only three of the four possible current state bits, Q3, Q2,
Q1, Q0.
12. (State Partitioning) Given
a 3-bit, eight-state Gray code up/down counter (similar to
the state machine in Figure 9.48), show how the state diagram
can be partitioned into two communicating finite state machines with five
states each, including idle states.
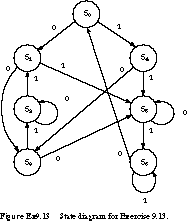
13. (State Partitioning) Given
the state diagram in Figure Ex9.13, partition the state machine into two
communicating finite state machines, one containing the states S0,
S1, S2, S3, and the other containing S4,
S5, S6.
14. (State Partitioning) Figure
Ex9.14 gives a state diagram with nine states.
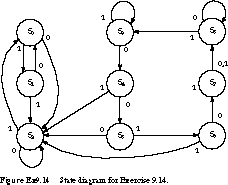
Show how to partition the state diagram into three communicating state
machines, consisting of the state groups S0, S1, S2;
S3, S4, S5; and S6, S7, S8.
15. (State Partitioning) The
partitioning rules presented in Figure 9.47 describe only the transformations
on states and transition conditions. Outputs are not considered.
Describe how the partitioning rules should be modified to handle Mealy outputs. How are the transfers into the idle states affected?16.
Describe how the partitioning rules should be modified to handle Moore outputs. How might the outputs from the partitioned machines be combined?
(Flip-Flop Choice) Given
the state diagram in Figure Ex9.16 and the state assignment S0
= 000, S1 = 001, S2 =
010, S3 = 011, S4 = 100, and
S5 = 101, do the following:
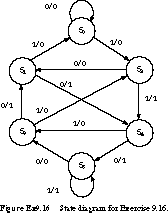
Write the encoded state table, and derive the minimized
Boolean equations for implementing the next-state and output functions.
Assume the state registers are implemented with D flip-flops.
Repeat the above, but this time using J-K
flip-flops.
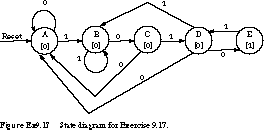
17. (Flip-Flop Choice) Given
the state diagram in Figure Ex9.17 and the state assignment A =
000, B = 001, C = 011, D
= 111, E = 101, implement the state machine
using a minimum number of gates and J-K flip-flops. You
may assume that an external RESET signal places the machine in state A
(000).
18. (Design Process) Implement
the following finite state machine description using a minimum number of
states and a good state assignment, assuming D flip-flops are used
for the state registers. The machine has a single input X, a single
output Z, and will assert Z = 1 for every
input sequence ending in the string 0010 or 100.
19. (Design Process) Your
task is to implement a finite state machine with toggle flip-flops given
the following state diagram. The finite state machine is actually a complex
Gray code counter. The counter has two control inputs, I1 and I0,
which determine the next state. The counter's functional specification is
as follows. When I1 I0 = 00, it is a Gray
code up-counter. When I1 I0 = 01, it is a
Gray code down-counter. When I1 I0 = 10,
it is a Gray code count by two. Finally, when I1 I0 =
11, the counter holds it current state. The state diagram is shown in Figure
Ex9.19.
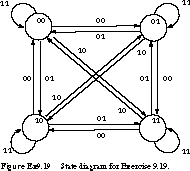
Complete a state transition table, including the next-state bits(Q1 and Q0)and the needed inputs to the two toggle state flip-flops T1 and T0 to obtain that next state.
Produce the four-variable K-maps for the next-state functions. Obtain the minimized two-level implementation.
Draw an implementation schematic, using a minimum number of inverters and two-input NAND, NOR, XOR, and XNOR gates. Assume that complements are not available.
(Design Process) Design
a Mealy finite state machine with input X and output Z.
The output Z should be asserted for one clock cycle whenever the
sequence 0111 or 1000 has been input on X. The patterns may overlap.
For example, X = 0000111000 should generate the output
stream Y = 0000001001.Complete the state diagram for the sequence detector, without concern for state minimization.
Complete the state table for the state diagram derived in part(a).
Use row matching or implication charts to minimize the state table derived in part(b).
Use the state assignment guidelines to obtain a good state assignment for the reduced state machine of part(c). Justify your method in terms of the high-, medium-, and low-priority assignment guidelines.
Implement your encoded, reduced state table using D flip-flops.
Implement your encoded, reduced state table using T flip-flops.
Implement your encoded, reduced state table using J-K flip-flops.