[Top] [Next]
[Prev]
9.1 Motivation for Optimization
To review, the finite state machine design process consists
of (1) understanding the problem, (2)
obtaining a formal description (ultimately, a symbolic
state transition table), (3)
minimizing the number of states, (4) encoding
the states, (5) choosing the flip-flops to implement
the state registers, and finally (6) implementing
the finite state machine's next-state and output functions. This chapter
starts at step 3 and carries us through to the final implementation at step
6, using methods based on discrete logic gates. We discuss the use of programmable
logic for finite state machine implementation in the next chapter.
9.1.1 Two State Diagrams, Same I/O Behavior
In the age of very large scale integrated circuits, why
should we bother to minimize a finite state machine implementation? After
all, as long as the input/output behavior of the machine is correct, it
really doesn't matter how it is implemented. Or does it?
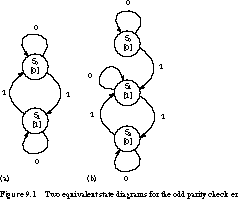
Figure 9.1 shows two different state diagrams for the odd parity checker
of Section 8.2. They have identical output behavior for all input strings.
You should try some inputs to convince yourself. We define equivalence
of finite state machines as follows. Two machines are equivalent if their
input/output behavior is identical for all possible input strings.
For a particular finite state machine, there are many
equivalent forms. Rather than reusing states while deriving the state diagram,
you could simply introduce a new state whenever you need one (to
keep the number of states finite, you will need to reuse some of them, of
course).
The two implementations of the state diagrams of Figure
9.1 are certainly not the same. The machine with more states requires more
flip-flops and more complex next-state logic.
9.1.2 Advantages of Minimum States
In general, you will find it is worthwhile to implement
the finite state machine in as few states as possible. This usually reduces
the number of logic gates and flip-flops you need for the machine's implementation.
Similarly, judicious mapping between symbolic and encoded
states can reduce the implementation logic. For the parity checker, our
implementation in Chapter 8 required no gates because we made a good state
assignment that naturally matched the control input to the toggle flip-flop.
A state diagram with n states must be implemented
with at least k flip-flops, where 2k - 1 < n ð
2k. By reducing the number of states to 2k - 1 or less, you can save a flip-flop.
For example, suppose you are given a finite state machine with five state
flip-flops. This machine can represent up to 32 states. If you can reduce
the number of states to 16 or less, you save a flip-flop.
Even when reducing the number of states is not enough
to eliminate a flip-flop, it still has advantages. With fewer states, you
introduce more don't-care conditions into the next-state and output functions,
making their implementation simpler. Less logic usually means shorter critical
timing paths and a higher clock rate for the system.
More important, today's programmable logic provides limited
gate and flip-flop counts on a single programmable logic chip. A typical
programmable logic part might have "2000 gate equivalents" (rarely
approached in practice) yet provide only 64 flip-flops! An
important goal of state reduction is to make the implementation "fit"
in as few components as possible. The fewer components you use, the shorter
the design time and the lower the manufacturing cost.
State reduction techniques also allow you to be sloppy
in obtaining the initial finite state machine description. If you have introduced
a few redundant states, you will find and eliminate them by using the state
reduction techniques introduced next.
[Top] [Next]
[Prev]
This file last updated on 07/15/96 at 06:40:56.
randy@cs.Berkeley.edu;

