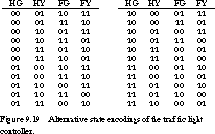
(4 factorial) = 4 * 3 * 2
* 1 = 24 different encodings (see Figure 9.19).

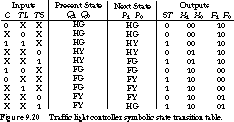
The input combinations that cause the state transitions are shown at
the left of the table. The symbolic state names HG, HY, FG, FY represent
the states highway green/farmroad red, highway yellow/farmroad red, highway
red/farmroad green, and highway red/farmroad yellow. We have already encoded
the traffic light outputs: 00 = Green, 01 = Yellow,
and 10 = Red.
We can use espresso to examine the alternative state assignments rapidly.

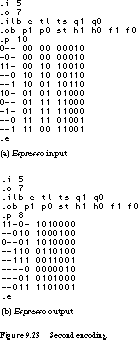
Figure 9.21 shows the generic truth table description that is input to
espresso. We simply replace the symbolic state names HG, HY, FG,
and FY with a particular encoding. Before we do a state assignment and two-level
minimization, the finite state machine requires 10 unique product terms
(one for each row of Figure 9.21).

Figure 9.22 and Figure 9.22 show the results of espresso runs
with the state assignments HG = 00, HY = 01, FG
= 11, FY = 10 and HG = 00, HY =
10, FG = 01, FY = 11 respectively. A cursory glance
shows that the second encoding uses fewer product terms, eight versus nine,
and fewer literals, 21 versus 26.
Comparison of the Two Encodings Let's look at the relative complexity of the two implementations. The logic equations implied by the two alternative encodings are the following.
With conventional gate logic, the encoding requires 3 five-input gates, 2 four-input gates, 6 three-input gates, and 2 two-input gates, a total of 13 gates. We assume that variables and their complements are available to the network.
This encoding requires 2 four-input gates, 8 three-input
gates, and 3 two-input gates, for a total of 13 gates. This implementation
uses the same number of gates, but it makes more extensive use of gates
with smaller fan-ins. This reduces overall wiring and is one reason why
it is often more useful to count literals than gates in comparing circuit
-complexity.
In the next two subsections, we present methods for finding
good state encodings. These are suitable for pencil and paper, as well as
computer-aided design tools.
State Maps State maps, similar in concept to K-maps, provide a means of observing adjacencies in state assignments. The squares of the state map are indexed by the binary values of state bits; the state given that encoding is placed in the map square. Obviously the technique is limited to situations in which a K-map can be used, that is, up to six -variables.
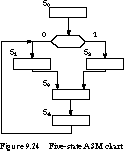
Figure 9.24 presents an ASM chart for a five-state finite state machine. Figure 9.25 gives two alternative state assignments and their representations in state maps.
Minimum-Bit-Change Heuristic One
heuristic strategy assigns states so that the number of bit changes for
all state transitions is minimized. For example, the assignment of Figure
9.25(a) is not as good as the one in Figure 9.25(b)
under this criterion:
| Transition | First Assignment Bit Changes | Second Assignment Bit Changes |
|---|---|---|
| S0 to S1: | 2 | 1 |
| S0 to S2: | 3 | 1 |
| S1 to S3: | 3 | 1 |
| S2 to S3: | 2 | 1 |
| S3 to S4: | 1 | 1 |
| S4 to S1: | 2 | 2 |
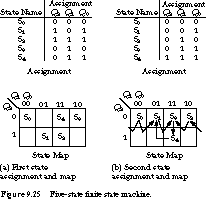
The first assignment leads to 13 different bit changes in the next-state function, the second only 7 bit changes.
We derived the first assignment completely at random
and the second assignment with minimum transition distance in mind. Here
is how we did it. We made the assignment for S0 first. Because
of the way reset logic works, it usually makes sense to assign all zeros
to the starting state. We make assignments for S1 and S2
next, placing them next to S0 because they are targets of transitions
out of the starting state.
Note how we used the edge adjacency of the state map.
This is so we can place S3 between the assignments for S1
and S2, since it is the target of transitions from both of these
states.
Finally, we place S4 adjacent to S3,
since it is the destination of S3's only transition. It would be
perfect if S4 could also be placed distance 1 from S0,
but it is not possible to do this and satisfy the other desired adjacencies.
The resulting assignment exhibits only seven bit transitions.
There may be many other assignments with the same number of bit transitions,
and perhaps an assignment that needs even fewer.
The minimum-bit-change heuristic, although simple, is
not likely to achieve the best assignment. For a finite state machine like
the traffic light controller, cycling through its regular sequence of states,
the minimum transition distance is obtained by a Gray code assignment: HG
= 00, HY = 01, FG = 11, FY =
10. This was the first state assignment we tried in the previous subsection,
and it was not as good as the second assignment, even though the latter
did not involve a minimum number of bit changes.
Guidelines Based on Next State and Input/Outputs Although
the criterion of minimum transition distance is simple, it suffers by not
considering the input and output values in determining the next state. A
second set of heuristic guidelines makes an effort to consider this in the
assignment of states:
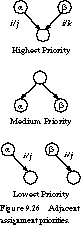
The guidelines, illustrated in Figure 9.26 for the candidate states a and b, are ranked from highest to lowest priority. The first two rules attempt to group together ones in the next-state maps, while the third rule performs a similar grouping function for the output maps. We do a state assignment by listing all state adjacencies implied by the guidelines, satisfying as many of these as possible.
Example Applying the Guidelines Consider
the state transition table of Figure 9.13 for the 3-bit sequence detector.
The corresponding state diagram is shown in Figure 9.27.
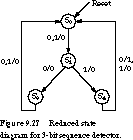
Let's apply the state assignment guidelines to this state diagram.The highest-priority constraint for adjacent assignment applies to states that share a common next state on the same input. In this case, states S3' and S4' both have S0 as their next state. No other states share a common next state.
The medium-priority assignment is for states that
have a common ancestor state. Again, S3' and S4'
are the only states that fit this -description.
The lowest-priority assignments are made for states that
have the same output behavior for a given input. S0, S1',
and S3' all output 0 when the input is 0. Similarly, S0,
S1', S3', and S4'
output 0 when the input is 1.
The constraints on the assignments can be summarized
as follows:
Highest priority:(S3', S4');
Medium priority:(S3', S4');
(S0, S1',
S3'); (S0, S1', S3',
S4');
Example Applying the Guidelines in a More Complicated
Case As another example, let's consider the more complicated
state diagram of the 4-bit string recognizer of Figure 9.7. Applying the
guidelines yields the following set of assignment constraints:
Highest priority:(S3', S4'),(S7', S10');
Medium priority:(S1, S2), 2 ¥(S3', S4'),(S7', S10');
(S0, S1,
S2, S3', S4', S7');(S0, S1, S2, S3',
S4', S7', S10');
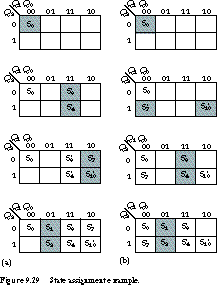
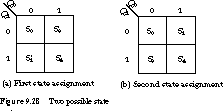
Figure 9.29 shows two alternative assignments that meet most of these
constraints. We start with Figure 9.29(a) and
first assign the reset state to the encoding for 0. Since (S3',
S4') is both a high-priority and medium-priority
adjacency, we make their assignments next. S3' is assigned
011 and S4' is assigned 111.
We assign (S7', S10')
next because this pair also appears in the high- and medium-priority lists.
We assign them the encodings 010 and 110, respectively. Besides giving them
adjacent assignments, this places S7 near S0, S3',
and S4', which satisfies some of the lower-priority -adjacencies.
The final adjacency is (S1, S2).
We give them the assignments 001 and 101. This satisfies a medium-priority
placement as well as the lowest--priority placements.
The second assignment is shown in Figure 9.29(b).
We arrived at it by a similar line of reasoning, except that we assigned
S7' and S10' the states 100 and 110.
The second assignment does about as good a job as the first, satisfying
all of the high- and medium-priority guidelines, as well as most of the
lowest-priority ones.
Applying the Guidelines: Why They Work The
state assignment guidelines attempt to maximize the adjacent groupings of
1's in the next-state and output functions. Let P2, P1,
and P0 be the next-state functions, expressed in terms of the current
state Q2, Q1, Q0 and the input X. To
see how effective the guidelines were, let's compare the assignment of Figure
9.29(a) with a more naive assignment: S0
= 000, S1 = 001, S2 =
010, S3' = 011, S4' =
100, S7' = 101, S10' =
110.
Figure 9.30 compares the encoded next-state tables and
K-maps for the two encodings. The 1's are nicely clustered in the next state
K-maps for the assignment derived from the guidelines. We can implement
P2 with three product terms and P1 and P2
with one each.
In the second assignment, the 1's are spread throughout
the K-maps, since we made the assignment with no attempt to cluster the
1's usefully. In this implementation, the next-state functions P2,
P1, and P0 each require three product terms, with a considerably
larger number of literals overall.
The state is encoded in four flip-flops rather than two, and only 1 bit is asserted in each of the states.HG=0001 HY=0010 FG=0100 FY=1000
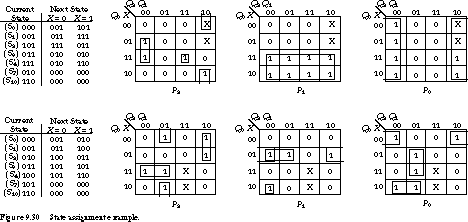
Figure 9.31 shows the espresso inputs and outputs for this encoding. It yields eight product terms, as good as the result of Figure 9.22. However, the logic is considerably more complex:

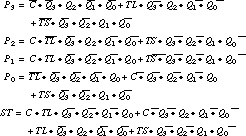
The product terms are all five and six variables, with two to five terms per output. This is rather complex for discrete logic but would not cause problems for a PLA-based design.
inputs current_state next_state outputs

(car sensor) is unasserted and the state
is HG (highway green), then the next state is
HG (highway green) and the outputs are 00010 (ST
= 0, H1:H0 = 00 "green," F1:F0 =
10 "red").
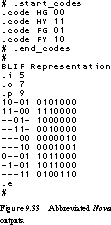
Figure 9.33 gives the abbreviated nova output associated with
the state machine of Figure 9.32, assuming you have requested a "greedy"
state assignment. The "codes" section shows the state assignment:
HG = 00, HY = 11, FG = 01, and FY
= 10. The espresso truth table is included in the
output, indicating that it takes nine product terms to implement the state
machine.
Intuitively, the state assignment algorithms used by
nova are much like the assignment guidelines of Section 9.3.2.
States that are mapped by some input into the same next state and that assert
the same output are partitioned into groups. In the terminology of state
assignment, these are called input constraints. Nova attempts
to assign adjacent encodings within the smallest Boolean cube to states
in the same group. A related concept is output constraints. States
that are next states of a common predecessor state are given adjacent assignments.
Nova implements a wide range of state-encoding
strategies, any of which you can select when you invoke the program:
(in other words, the literal count may be
greatly reduced). (the one requiring the
smallest number of product terms).
None of the assignments found by nova match the eight-product-term encoding we found in Figure 9.22. But we shouldn't despair just because the tool did not find the best possible assignment. The advantage of the computer-based tool is that it finds reasonable solutions rapidly. Thus you can examine a variety of encodings and choose the one that best reduces your implementation task.
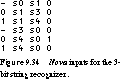

As another example, let's consider the 3-bit sequence recognizer of Figure 9.27. Its nova input file is shown in Figure 9.34. The state assignments found by nova are the following:
Several of the assignments correspond to the ones
found in Figure 9.28(a) and (b).
The last example is the 4-bit recognizer of Figure 9.7. The nova input file is given in Figure 9.35. Nova produced the following -assignments:
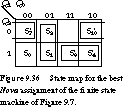
None of these assignments match those derived in Figure 9.29, since S0 has not been assigned 000. Figure 9.36 shows that the adjacencies that were highly desirable based on the guidelines-that is, S3' adjacent to S4', S7' adjacent to S10', and S1 adjacent to S2-are satisfied by the input annealing assignment.
Mustang The minimum number of product terms is a good criterion if you are going to implement the logic in a two-level form, such as a PLA. This is what nova uses. Literal count is better if you plan to implement the logic in multiple levels. Mustang takes this approach. Its optimization criterion is to minimize the number of literals in the multilevel factored form of the next-state and output functions.
Mustang has an input format similar to that
of nova. The only difference is that the number of inputs, outputs,
and state bits must be explicitly declared with .i, .o,
and .s directives. For example, the traffic light input file
is shown in Figure 9.37.

Mustang implements several alternative strategies for state assignment, specified by the user on the command line. These include:
| | HG | HY | FG | FY | Number of product terms |
|---|---|---|---|---|---|
| Random: | 01 | 10 | 11 | 00 | 9 |
| Sequential: | 01 | 10 | 11 | 00 | 9 |
| Fan-in: | 00 | 01 | 10 | 11 | 8 |
| Fan-out: | 10 | 11 | 00 | 01 | 8 |
The eight term encodings are actually better than any of those found by nova. To determine the multilevel implementation, you must invoke misII on the espresso file created by mustang.
For example, the misII output for the fan-in encoding of the traffic light controller is the following:
For comparison with nova, mustang obtains the following encodings for the 3-bit string recognizer:
| | S0 | S1 | S3' | S4' | Number of product terms |
|---|---|---|---|---|---|
| Random: | 01 | 10 | 11 | 00 | 5 |
| Sequential: | 01 | 10 | 11 | 00 | 5 |
| Fan-in: | 10 | 11 | 00 | 01 | 4 |
| Fan-out: | 10 | 11 | 00 | 01 | 4 |
The number of product terms to implement an encoding is comparable to the number needed for the nova encodings. However, don't forget that the goal of mustang is to reduce literal count rather than product terms.
As a final example, let's look at the mustang encodings for the 4-bit recognizer:
It is interesting that in all three cases, mustang
obtained an encoding that is as good as any of the best encodings found
by nova.
Jedi The final encoding program we shall examine
is jedi. It is similar to mustang in that its goal is
to obtain a good encoding for a multilevel implementation. It is more powerful
than mustang because it can solve general encoding problems:
jedi can find good encodings for the outputs as well as the states.
Like the other programs, jedi implements several
alternative encoding strategies that can be selected on the command line.
Besides random, one hot, and straightforward, the program supports input
dom-i-nant, output dominant, modified output dominant, and input/output
combination algorithms.
The jedi input format is similar to, but slightly
different from, the mustang input format. We can illustrate this
best with an example. Figure 9.38 shows the jedi input file for
the traffic light controller. The present state and next states each count
as a single input, even though they may be encoded by several bits. The
.enum States line tells jedi that there are four states
and that they should be encoded in 2 bits and then gives the state names.
The .enum Colors line tells jedi that there are three
output colors and that these should also be encoded in 2 bits. You should
think of these as enumerated types. The .itype and .otype
lines define the types of the inputs and outputs, respectively.
The encodings obtained from jedi for the traffic light controller are:
| | HG | HY | FG | FY | Grn | Yel | Red | Number of product terms |
|---|---|---|---|---|---|---|---|---|
| Input: | 00 | 10 | 11 | 01 | 11 | 01 | 00 | 9 |
| Output: | 00 | 01 | 11 | 10 | 10 | 11 | 01 | 9 |
| Combination: | 00 | 10 | 11 | 01 | 10 | 00 | 01 | 9 |
| Output': | 01 | 00 | 10 | 11 | 10 | 00 | 01 | 10 |
For the 3-bit string recognizer, the state assignments are:
| | S0 | S1 | S3' | S4' | Number of product terms |
|---|---|---|---|---|---|
| Input: | 01 | 00 | 11 | 10 | 4 |
| Output: | 11 | 01 | 00 | 10 | 4 |
| Combination: | 10 | 00 | 11 | 01 | 4 |
| Output': | 11 | 01 | 00 | 10 | 4 |
Finally, for the 4-bit string recognizer, they are:
Let's look at one head-to-head comparison between
mustang and jedi. We will use the mustang encoding
in which HG = 00, HY = 01, FG = 10,
FY = 11, Green = 00, Yellow = 01,
and Red = 10 and the jedi encoding in which HG =
00, HY = 01, FG = 11, FY = 10, Green
= 10, Yellow = 11, and Red = 01.
The first encoding used eight product terms in a two-level implementation;
the second used nine.

The multilevel implementation for the mustang assignment was already shown in the mustang section. It requires 26 literals. The jedi multilevel implementation is
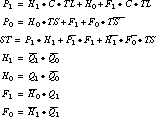
It has 27 literals. In terms of straight literal count,
the mustang encoding is better. If we examine the wiring complexity,
the mustang encoding is also slightly better.
[Top] [Next]
[Prev]