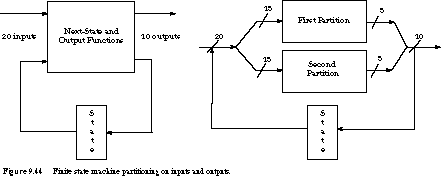
Example 1 FSM Partitioning To illustrate
the value of state machine partitioning, suppose we have a finite state
machine with 20 inputs and 10 outputs (including next-state
outputs). But we only have programmable logic components with
15 inputs and 5 outputs. We cannot implement this finite state machine with
a single component.
Of course, it isn't always possible to find such a fortuitous partitioning.
For example, every output might be a function of 16 inputs.
If we cannot reduce the complexity of the finite state
machine by simple input/output partitioning, another way to "make it
fit" is to partition the single finite state machine into smaller,
less complex, communicating finite state machines. We examine this approach
in the next subsection.
Example 2 FSM Partitioning For
example, Figure 9.45 shows a subset of a state diagram.
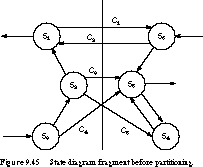
We have chosen to partition the state diagram into two separate machines,
containing states S1, S2, S3 and S4,
S5, S6, respectively. The symbols Ci associated
with the transitions represent the Boolean conditions under which the transition
takes place.
What happens if we partition the state diagram, but a
transition must take place between the two pieces? We need to introduce
idle states to synchronize the activity between the two finite state machines.
In essence, the machine at the left hands control off to the machine at
the right when a transition from S1 to S6 takes place.
The left machine must idle in some new state until it regains control, such
as when there is a transition from S6 back to S1. In this
event, the machine on the right must remain idle until it regains control.
The revised state diagrams are shown in Figure 9.46.
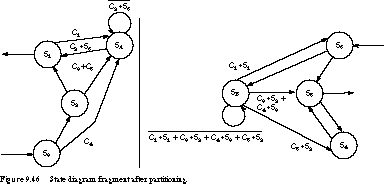
We have introduced two new states, SA and SB, to synchronize
the transitions across the partition boundary. Here is how it works for
the state sequence S1 to S6 and back to S1. Initially,
the machines are in states S1 and SB. If condition C1
is true, then the left-hand state machine exits S1 and enters its
idle state, SA. At the same time, the right-hand machine exits
SB and enters S6.
Suppose that the right-hand machine sequences through
some states, eventually returning to S6. Throughout this time,
the left-hand machine remains in its idle state. If the right-hand machine
is in S6 and C2 is true, it next enters its idle state,
SB. At the same instant, the left-hand machine exits SA,
returning to S1. While the left-hand machine sequences through
states, the right-hand machine idles in SB.
Rules for Partitioning We are ready
to describe the rules for introducing idle states into a partitioned finite
state machine. We illustrate each rule with an example from the partitioned
state machine of the previous subsection. All the rules involve transitions
that cross the partition -boundary.
The first rule applies for a state that is the source
of a transition that crosses the boundary. The case is shown in Figure 9.47(a).
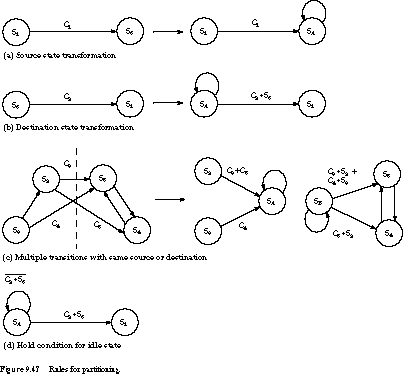
The cross-boundary transition is replaced by a transition to the idle
state, labeled by the same exit condition as the original transition. For
example, the S1-to-S6 transition is replaced by a transition
with the same condition to SA.
The second rule applies to the destination of a transition
that crosses the partition boundary. This is shown in Figure 9.47(b).
The transition is replaced with an exit transition from the idle state,
labeled with the original condition ANDed with the source state. For example,
the transition from S6 to S1 is replaced with a transition
from SA. We exit the idle state when both C2 is true and
the right-hand state machine is in S6. Hence, the transition is
labeled with the condition C2 S6.
The third rule applies when multiple transitions share
the same source or destination. This case is illustrated in Figure 9.47(c).
If a state is the source of multiple transitions across the partition boundary,
all of these are collapsed into a single transition to the idle state. The
exit conditions are ORed together to label the new transition. For example,
S2 has transitions to states S5 and S4. These
are replaced with a single transition to SA, labeled C3
+ C5.
If a state is the target of multiple transitions across
the boundary, a single transition is added from the idle state to this state.
The transition is labeled with the OR of the conditions associated with
the individual transitions in the original state machine. This case is illustrated
by the transitions from S2 and S3 to S5. These
are replaced by a single transition from SB to S5, labeled
C3 S2 + C4 S3.
When all these rules have been applied, the final rule
describes the self-loop ("hold") condition
for the idle states. Simply form the OR of all of the exit conditions and
invert it. This is shown in Figure 9.47(d). Consider
the idle state SA. Its only exit condition is C2 S6.
So its hold condition is the inverse of this, namely ![]() .
.
Example 3 FSM Partitioning Consider
the six-state finite state machine of Figure 9.48(a).
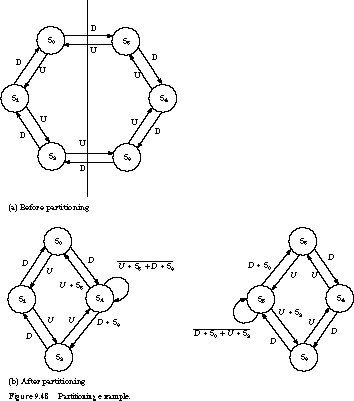
The machine implements a simple up/down counter. When the input U
is asserted, the machine counts up. When D is asserted, it counts
down. Otherwise the machine stays in its current state.
The goal is to partition the machine into two communicating
four-state finite state machines. We might need to do this because the underlying
logic primitives provide support for two flip-flops within the logic block,
as in the Xilinx CLB to be introduced in the next chapter.
Figure 9.48(b) shows the result
of the partitioning. States S0, S1, and S2 form
the core of one machine and S3, S4, and S6 form
the other. We also introduce the two idle states, SA and SB.
The machine at the left enters its idle state SA
when it is in S0 and D is asserted or when it is in S2
and U is asserted. It exits the idle state when the machine at
the right is in S5 with U asserted or in S3 with
D asserted. Otherwise it stays in its idle state. The machine at
the right works similarly.
To see how the machines communicate, let's consider an
up-count sequence from S0 to S5 and back to S0.
On reset, the machine on the left enters S0 while the machine on
the right enters SB. With U asserted, the left machine
advances from S0 to S1 to S2 to SA.
It will idle in this state until the right machine is ready to exit S5.
Meanwhile, the right machine holds in SB until
the left machine enters S2. At the same time that the left machine
changes to SA, the right one exits SB to S3.
On subsequent clock transitions, it advances from S3 to S4
to S5 to SB, where it holds. When the right machine changes
from S5 to SB, the left machine exits SA to S0,
and the process repeats itself. Down-count sequences work in an analogous
way.
[Top] [Next]
[Prev]